Root Locus MCQ

Root Locus MCQ

Root Locus MCQ, Multiple Choice Questions on Root Locus in Control System, Objective Questions on Control System, Gate Questions on Root Locus, Root Locus Objective Questions with Answer, Root Locus MCQ with the answer, Engineering MCQ, Control System MCQ

Objective Type Questions

Q.1. The root-locus diagram for a closed-loop feedback system is shown in the figure below. The system is overdamped.

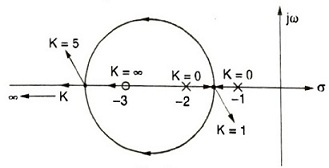
• only if 0 ≤ K ≤ 1
• only if 1 < K < 5
• only if K > 5 
• if 0 ≤ K ≤ 1 or K > 5

Answer: if 0 ≤ K ≤ 1 or K > 5

Q.2. The root locus of the system G(s)H(s)=\frac{K}{s(s+2)(s+3)} has the break away point located at

• (- 0.5, 0)
• (- 2.548, 0)
• (- 4. 0)
• (- 0.784, 0)

Answer: (- 0.784, 0)

Q.3. Given G(s)H(s)=\frac{K}{s(s+1)(s+3)}, the point of interaction of the asymptotes of the root loci with the real axis is

• – 4
• 1.33
• – 1.33
• 4

Answer: – 1.33

Q.4. A unity feedback control system has an open loop transfer function

G(s)=\frac{K}{s(s^{2}+7s+12)}

The gain K for which s = -1 + j1 will lie on the root locus of this system is

• 4
• 5.5
• 6.5
• 10

Answer: 10

Q.5. The feedback configuration and the pole zero location of

G(s)=\frac{s^{2}-2s+2}{s^{2}+2s+2}

are shown below. The root locus for negative values of K. i.e. for – ∞ < K < 0 has breakaway/break in points and angle of departure at pole P (with respect to the positive real axis) equal to 

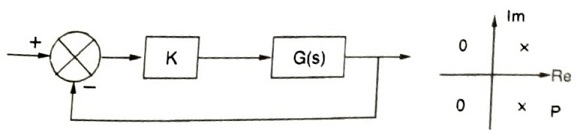
• \pm \sqrt{2} and 0°
• \pm \sqrt{2} and 45°
• \pm \sqrt{3}  and 0°  
• \pm \sqrt{3} and 45°

Answer: \pm \sqrt{2} and 45°

Q.6. The root locus plot for a system is given below. The open loop transfer function corresponding to this plot is given by

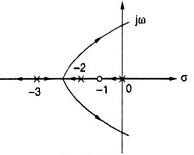
• G(s)H(s)=K\frac{s(s+1)}{(s+2)(s+3)}
• G(s)H(s)=K\frac{(s+1)}{s(s+2)(s+3)^{2}}
• G(s)H(s)=K\frac{1}{s(s-1)(s+2)(s+3)}
• G(s)H(s)=K\frac{(s+1)}{s(s+2)(s+3)}

Answer: G(s)H(s)=K\frac{(s+1)}{s(s+2)(s+3)^{2}}

Q.7. Consider the points s₁ = – 3 + j4 and s₂ = – 3 – j2 in the s-plane. Then, for a system with the open loop transfer function G(s)H(s)=\frac{K}{(s+1)^{4}}.

• s₁ is on the root locus, but not s₂
• s₂ is on the root locus, but not s₁
• both s₁ and s₂ are on the root locus
• Neither s₁ nor s₂ is on the root locus

Answer: both s₁ and s₂ are on the root locus

Q.8. For a unity negative feedback control system, the open-loop transfer function

G(s)=\frac{K}{s(s+1)(s+2)}.

The root locus plot of the system is

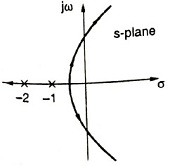
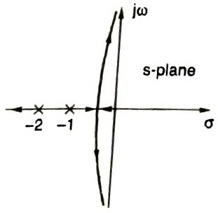
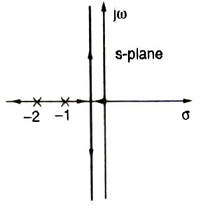
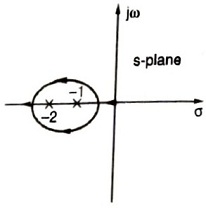
Answer: 1st figure

Q.9. The intersection of root-loci of asymptotes of a system with open loop transfer function

G(s)H(s)=\frac{K}{s(s+1)(s+3)} is

• 1.44
• 1.33
• – 1.44
• – 1.33

Answer: – 1.33

Q.10. The root locus plot of the system having the loop transfer function 

G(s)H(s)=\frac{K}{s(s+4)(s^{2}+4s+5)} has

• no breakaway point
• three real breakaway points
• only one breakaway point
• one real and two complex breakaway points

Answer: three real breakaway points

Q.11. Which of the following is the open-loop transfer function of the root loci shown in the figure below?

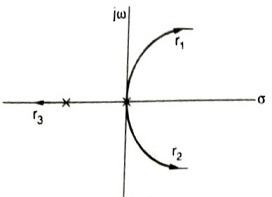
• \frac{K}{s(s+T_{1})^{2}}
• \frac{K}{(s+T_{1})(s+T_{2})^{2}}
• \frac{K}{(s+T_{1})^{3}}
• \frac{K}{s^{2}(sT_{1}+1)}

Answer: \frac{K}{s^{2}(sT_{1}+1)}

Q.12. The instrument used for plotting the root locus is called

• slide rule
• spirule
• synchro
• selsyn 

Answer: spirule

Q.13. The below figure shows the root locus of a unity feedback system. The open loop transfer function of the system is

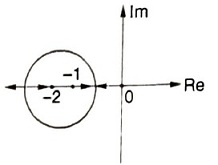
• \frac{K}{s(s+1)(s+2)}
• \frac{Ks}{(s+1)(s+2)}
• \frac{K(s+1)}{s(s+2)}
• \frac{K(s+2)}{s(s+1)}

Answer: \frac{K(s+2)}{s(s+1)}

Q. 14. Which one of the following application software is used to obtain an accurate root locus plot ?

• LISP
• MATLAB
• D Base
• Oracle

Answer: MATLAB

Q.15. The root loci of a feedback control system for large values of s are asymptotic to the straight lines with angles θ to the real axis given by which one of the following ?

• \frac{(p-z)\pi }{2k+1}
• \frac{(2k+1)\pi }{p-z}
• 2k(p-z)
• \frac{2k}{p}z

Answer: \frac{(2k+1)\pi }{p-z}

where p = Number of finite poles of G(s) H(s), z = Number of finite zeros of G(s) H(s) and k = 0, 1, 2, …

Q 16. Which one of the following is not a property of root loci ?

• The root locus is symmetrical about jω axis.
• They start from the open-loop poles and terminate at the open-loop zeros.
• The breakaway points are determined from dk/ds = 0
• Segments of the real axis are part of the root locus, if and only if, the total  number of real poles and zeros to their right is odd

Answer: The root locus is symmetrical about jω axis.

Q. 17. For a given unity feedback system with G(s)H(s)=\frac{k(s+3)}{s(s+1)(s+2)(s+5)}, what is the real axis intercept for root locus asymptotes?

• 2/3
• 1/4
• -5/3
• – 3/2

Answer: -5/3

Q.18. Which one of the following open loop transfer functions has root locus parallel to imaginary axis?

• K/(s + 1)
• K(s + 1)/(s + 2)²
• K/(s + 2)²
• K(s + 2)/(s + 1)²

Answer: K/(s + 2)²

Q.19. Consider the root loci plots:

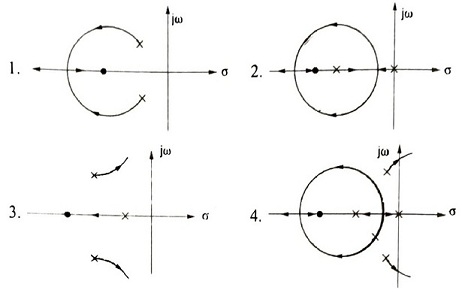
which one of the above plots is not correct

• 1
• 2
• 3
• 4

Answer: 4

Q.20. The addition of open loop zero pulls the root loci towards

• The left and therefore system becomes more stable
• The right and therefore system becomes unstable
• Imaginary axis and therefore system becomes marginally stable
• The left and therefore system becomes unstable

Answer: The left and therefore system becomes more stable

Related Posts:

Bode Plot MCQ – Control Engineering

Routh Hurwitz (RH) Criterion MCQ