Discrete Convolution and Correlation MCQ

Discrete Convolution and Correlation MCQ

Discrete Convolution and Correlation MCQ, Multiple Choice Questions on Discrete Convolution and Correlation, Discrete Convolution MCQ, Discrete Correlation MCQ, Digital Signal Processing MCQ, DSP MCQ, Engineering MCQ

Discrete-Time Signals and Systems MCQ

Objective Type Questions

Q.1. The commutative property of convolution states that

• x(n) *h(n) = h(n) *x(n)
• [ x(n) *h₁ (n)] *h₂ (n) = x(n) * [h₁ (n) *h₂ (n)]
• x(n) * [h₁(n) + h₂ (n)] = x(n) *h₁(n) + x(n) *h₂ (n)
• none of these

Answer: x(n) *h(n) = h(n) *x(n)

Q.2. The associate property of convolution states that

• x(n) *h(n) = h(n) *x(n)
• [x(n) *h₁ (n)] *h₂ (n) = x(n) * [h₁ (n) *h₂ (n)]
• x(n) * [h₁(n) + h₂ (n)] = x(n) *h₁(n) + x(n) *h₂ (n)
• none of these

Answer: [ x(n) *h₁ (n)] *h₂ (n) = x(n) * [h₁ (n) *h₂ (n)]

Q.3. The distributive property of convolution states that

• x(n) *h(n) = h(n) *x(n)
• [ x(n) *h₁ (n)] *h₂ (n) = x(n) * [h₁ (n) *h₂ (n)]
• x(n) * [h₁(n) + h₂ (n)] = x(n) *h₁(n) + x(n) *h₂ (n)
• none of these

Answer: x(n) * [h₁(n) + h₂ (n)] = x(n) *h₁(n) + x(n) *h₂ (n)

Q.4. For a non-causal system h(n) excited by a non-causal input x(n), the output y(n) is given by

• y(n)=\sum_{k=-\infty }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=-\infty }^{n }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{n }x(k)h(n-k)

Answer: y(n)=\sum_{k=-\infty }^{\infty }x(k)h(n-k)

Q.5. For a non-causal system h(n) excited by a causal input x(n), the output y(n) is given by

• y(n)=\sum_{k=-\infty }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=-\infty }^{n }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{n }x(k)h(n-k)

Answer: y(n)=\sum_{k=0 }^{\infty }x(k)h(n-k)

Q.6. For a causal system h(n) excited by a non-causal input x(n), the output y(n) is given by

• y(n)=\sum_{k=-\infty }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=-\infty }^{n }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{n }x(k)h(n-k)

Answer: y(n)=\sum_{k=-\infty }^{n }x(k)h(n-k)

Q.7. For a causal system h(n) excited by a causal input x(n), the output y(n) is given by

• y(n)=\sum_{k=-\infty }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{\infty }x(k)h(n-k)
• y(n)=\sum_{k=-\infty }^{n }x(k)h(n-k)
• y(n)=\sum_{k=0 }^{n }x(k)h(n-k)

Answer: y(n)=\sum_{k=0 }^{n }x(k)h(n-k)

Q.8. If x(n) = {1, 2, 3, 0} and h(n) = {3, 1, 0, 0, 0}, the length of y(n) = x(n) * h(n) is

• 8
• 7
• 9
• none of these

Answer: 8

Q.9. {1, 2, 3} * {3, 2, 1} =

• {3, 8, 1, 4, 8, 3}
• {3, 8, 8, 3}
• {3, 8, 12, 8, 3}
• {2, 3, 8, 14, 8, 3}

Answer: {3, 8, 1, 4, 8, 3}

Q.10.

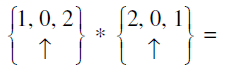
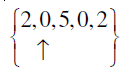
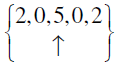
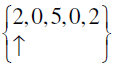
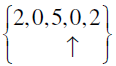
Answer:

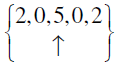
Q.11. [x(n) = {δ (n +2) - δ (n) + δ (n -2)}] *[h(n) = { δ (n) + δ (n -1)}] is

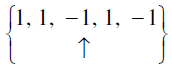
none of these

Answer:

Q.12. The convolution of x(n) = {1, 2, 0, 0, 0} and h(n) = {2, 1, 0} is

• {2, 5, 2, 0, 0, 0}
• {2, 5, 2, 0, 0, 0, 0}
• {2, 5, 0, 0, 0, 0, 0}
• {2, 5, 1, 0, 0, 0, 0}

Answer: {2, 5, 2, 0, 0, 0, 0}

Q.13. If x(n) = {1, 2, 3, 0, 4, 0, 6}, then circularly shifted signal x(n – 2) =

• {0, 6, 1, 2, 3, 0, 4}
• {0, 0, 1, 2, 3, 0, 4}
• {0, 0, 1, 2, 3, 0, 4, 0, 6}
• {-1, 0, 1, 0, 2, 0, 4}

Answer: {0, 6, 1, 2, 3, 0, 4}

Q.14. If x(n) = {1, 2, 3, 0, 4, 0, 6}, then circularly shifted signal x(n + 2) =

• {1, 2, 3, 0, 4, 0, 6, 0, 0}
• {3, 0, 4, 0, 6, 1, 2}
• {3, 4, 5, 0, 6, 0, 8}
• {0, 0, 1, 2, 3, 0, 4, 0, 6}

Answer: {3, 0, 4, 0, 6, 1, 2}

Q15. If x(n) = {1, 2, 3, 0, 4, 0, 6}, then circularly flipped signal x(–n) =

• {1, 6, 0, 4, 0, 3, 2, 1}
• {6, 0, 4, 0, 3, 2, 1}
• {-1, -2, -3, 0, -4, 0, -6}
• none of these

Answer: {1, 6, 0, 4, 0, 3, 2, 1}

Q.16. The circular convolution of x(n) = {1, 2, 1} and h(n) = {2, 1, 2} is

• {7, 7, 6}
• {6, 7, 6}
• {6, 7, 6, 0}
• {0, 7, 7, 6}

Answer: {7, 7, 6}

Q.17. What is the periodic extension of x(n) = {1,0,2,0,3,0,4} for period N = 3?

• {2, 3, 5}
• {5, 3, 2}
• {1, 2, 3}
• {1, 0, 2}

Answer: {5, 3, 2}

Q.18. What is the periodic extension of x(n) = {2, 2} for N = 3?

• {2, 2, 0}
• {0, 2, 2}
• {2, 2, 2}
• {0, 2, 2, 0}

Answer: {2, 2, 0}

Q.19. The cross correlation of x(n) = {1, 2, 1} and h(n) = {1, 2} is

• {1, 4, 5, 2}
• {2, 5, 4, 1}
• {1, 2, 1, 1, 2}
• {1, 3, 5, 2}

Answer: {2, 5, 4, 1}

Q.20. The autocorrelation of x(n) = {2, 1} is

• {2, 5, 2}
• {4, 4, 1}
• {2, 1}
• {2, 1, 2, 1}

Answer: {2, 5, 2}