Routh Hurwitz (RH) Criterion MCQ
Routh Hurwitz (RH) Criterion MCQ, Routh Hurwitz Criterion MCQ, RH Criterion MCQ, MCQ on RH Criterion, Objective Questions on Routh Hurwitz (RH) Criterion, Objective Questions on RH Criterion, Engineering MCQ, Control System MCQ
Questions Type Questions
Q.1. A system described by the transfer function:
G(s)=\frac{1}{s^{3}+\alpha s^{2}+Ks+3} is stable
The constraints on α and K are
- \alpha > 0, \alpha K< 3
- \alpha > 0, \alpha K> 3
- \alpha < 0, \alpha K> 3
- \alpha < 0, \alpha K< 3
Answer: \alpha > 0, \alpha K> 3
Q.2. The feedback control system in the figure below is stable
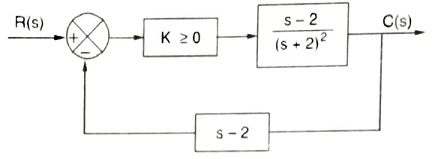
- for all K≥0
- only K≥0
- only if 0≤ K < 1
- only if 0 ≤ K ≤ 1
Answer: only if 0≤ K < 1
Q.3. The characteristic polynomial of a system is q(s)=2s^{5}+s^{4}+4s^{3}+2s^{2}+2s+1. The system is
- Stable
- Marginally stable
- Unstable
- Oscillatory
Answer: Unstable
Q.4. The open-loop transfer function of a unity feedback system
G(s)=\frac{K}{s(s^{2}+s+2)(s+3)}The range of K for which the system is stable is
- \frac{21}{4}> K> 0
- 13> K> 0
- \frac{21}{4}< K< \infty
- -6< K< \infty
Answer: \frac{21}{4}> K> 0
Q.5. For the polynomial:
P(s)=s^{5}+s^{4}+2s^{3}+2s^{2}+3s+15, the number of roots which lie in the right half of the s-plane is
- 4
- 2
- 3
- 1
Answer: 2
Q. 6. The Positive values of “K” and ‘a’ so that the system shown in the figure below oscillates at a frequency of 2 rad/sec respectively are

- 1, 0.75
- 2, 0.75
- 1, 1
- 2, 2
Answer: 2, 0.75
Q.7. A certain system has transfer function G(s)=\frac{s+8}{s^{2}+\alpha s-4}, where α is a parameter. Consider the standard negative unity feedback configuration as shown below:
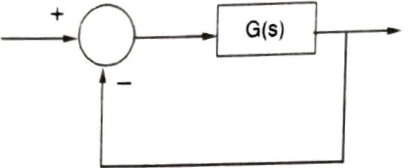
Which of the following statements is true ?
- The closed-loop system is never stable for any value of α
- For some positive values of α, the closed-loop system is stable, but not for all positive values.
- For all positive values of α, the closed-loop system is stable.
- The closed-loop system is stable for all values of α, both positive and negative.
Answer: For all positive values of α, the closed-loop system is stable.
Q.8. The number of open right half plane poles of
G(s)=\frac{10}{s^{5}+2s^{4}+3s^{3}+6s^{2}+5s+3}- 0
- 1
- 2
- 3
Answer: 2
Q.9. The open-loop transfer function of unity feedback control system is G(s)=\frac{K}{s(s+a)(s+b)}, 0< a\leq b
The system is stable is
- 0< K< \frac{(a+b)}{ab}
- 0< K< \frac{ab}{(a+b)}
- 0< K< ab(a+b)
- 0< K< \frac{a}{b}(a+b)
Answer: 0< K< ab(a+b)
Q.10. The Routh-Hurwitz criterion cannot be applied when the characteristic equation of the system contains any coefficients which is
- negative real and exponential functions of s
- negative real, both exponential and sinusoidal function of.s.
- both exponential and sinusoidal functions of s
- complex, both exponential and sinusoidal functions of s.
Answer: negative real, both exponential and sinusoidal function of.s.
Q.11. The given characteristic polynomial s^{4}+s^{3}+2s^{2}+2s+3=0 has
- zero roots in RHS of s-plane
- one root in RHS of s-plane
- two roots in RHS of s-plane
- three roots in RHS of s-plane
Answer: two roots in RHS of s-plane
Q.12. The characteristic equation of a control system is given by s^{6}+2s^{5}+8s^{4}+12s^{3}+20s^{2}+16s+16=0. The number of the roots of the equation which lie in the imaginary axis of s-plane is
- zero
- 2
- 4
- 6
Answer: 4
Q.13. An open loop system has a transfer function \frac{1}{s^{3}+1.5s^{2}+s-1}. it is converted into a closed loop system by providing a negative feedback having 20(s + 1). Which one of the following is correct?
The open loop and closed loop system are, respectively
- stable and stable
- stable and unstable
- unstable and stable
- unstable and unstable
Answer: unstable and stable
Q.14. The open loop transfer function of a unity negative feedback control system is given by
G(s)=\frac{k}{(s+2)(s+4)(s^{2}+6s+25)}Which is the value of k which causes sustained oscillations in the closed loop system?
- 666.25
- 790
- 990
- 1190
Answer: 666.25
Q.15. The unit step response of a system is 1-e^{-t}(1+t). Which is this system?
- Unstable
- Stable
- Critically stable
- Oscillatory
Answer: Stable
Q.16. The system having characteristic equation:
s^{4}+2s^{3}+3s^{2}+2s+K=0 is to be used as an oscillator. What are the values of k and the frequency of oscillation ω?
- k = 1 and ω = 1 r/s
- k = 1 and ω = 2 r/s
- k = 2 and ω = 1 r/s
- k = 2 and ω = 2 r/s
Answer: k = 2 and ω = 1 r/s
Q.17. The characteristic equation of a control system is
s^{5}+15s^{4}+85s^{3}+225s^{2}+274s+120=0What are the number of roots of the equation which lie to the left of the line s+1=0 ?
- 2
- 3
- 4
- 5
Answer: 3
Q.18. The open loop transfer function of a unity feedback control system is given by
G(s)=Ke^{-Ts}Where K and T are variables and are greater than zero. The stability of the closed loop system depends on
- K only
- Both K and T
- T only
- Neither K nor T
Answer: T only
Q. 19. Consider the unity feedback system with G(s)=\frac{K}{(s^{2}+2s+2)(s+2)}
The system is marginally stable. What is the radian frequency of oscillation?
- \sqrt{2}
- \sqrt{3}
- \sqrt{5}
- \sqrt{6}
Answer: \sqrt{6}
Q.20. For what positive value of K does the polynomial
s^{4}+8s^{3}+24s^{2}+32s+Khave roots with zero real parts ?
- 10
- 20
- 40
- 80
Answer: 80
Q.21. The characteristics equation of a control system is given as
s^{4}+8s^{3}+24s^{2}+32s+K=0What is the range of values of K for this system to be stable ?
- 0 ≤ K < 80
- 0 ≤ K < 100
- 0 ≤ K < 300
- 0 ≤ K < 600
Answer: 0 ≤ K < 80