MCQ on Probability & Random Signal Theory

MCQ on Probability & Random Signal Theory

MCQ on Probability & Random Signal Theory, Objective Questions on Probability & Random Signal Theory, Gate questions on Probability & Random Signal Theory, Probability MCQ, Random Signal Theory MCQ, Probability & Random Signal Theory MCQ

Multiple-Choice Questions

1. Which of the following is incorrect?

• A-B=A\bar{B}
• \bar{AB}=\bar{A}\bar{B}
• A.\bar{A}=0
• A.A=A

Answer: \bar{AB}=\bar{A}\bar{B}

2. Pick the odd one out among

• stochastic variable
• stochastic function
• random variable
• random experiment

Answer: random experiment

3. Pick the odd one out among

• binomial distribution
• normal distribution
• uniform distribution
• Rayleigh distribution

Answer: binomial distribution

4. Which of the following is incorrect?

• P(S)= 1
• P(\bar{A})=P(A)-1
• 0\leq P(A)\leq 1
• If A and B are mutually exclusive, then P(A + B) = P(A) + P(B)

Answer: P(\bar{A})=P(A)-1

5. The total area under the probability distribution curve is

• 1
• 0
• depends on the nature of the distribution
• none of the above

Answer: 1

6. The spectral density of white noise

• varies with frequency
• varies with bandwidth
• varies with the amplitude of the signal
• is constant

Answer: is constant

7. The theoretical power of white noise is

• zero
• finite
• infinite
• depends on the frequency of the signal

Answer: depends on the frequency of the signal

8. The stationary process has

• ensemble average equal to time average
• all the statistical properties dependent on time
• all the statistical properties independent of time
• zero variance

Answer: all the statistical properties independent of time

9. Events A and B are statistically independent if

• A and B occur simultaneously
• A and B occur at different times
• occurrence of A includes occurrence of B
• none of the above

Answer: none of the above

10. Pick the odd man out among

• expectation
• variance
• standard deviation
• Tchebycheff’s inequality

Answer: Tchebycheff’s inequality

11. The probability density function of a random variable X is ae^{-bx}u(x). Then

• a and b can be arbitrary
• a = b/2
• a = b
• a = 2b

Answer: a = b/2

12. The density function of a random variable X is given by: f(x)=\left\{\begin{matrix} \frac{1}{b-a}, & a\leq x\leq b\\ 0, & otherwise \end{matrix}\right.

The variable X is said to have

• Poisson distribution
• Gaussian distribution
• Rayleigh distribution
• uniform distribution

Answer: uniform distribution

13. The probability density function of a random variable is given by p(x)=ke^{-x^{2}}  -∞≤x≤∞. The value of k should be 

• \frac{1}{\sqrt{2\pi }}
• \sqrt{\frac{2}{\pi}}
• \frac{1}{2\sqrt{\pi }}
• \frac{1}{\pi \sqrt{2}}

Answer: \frac{1}{\sqrt{2\pi }}

14. For a random various x with probability function p_(x) shown in the following figure, the mean and the variance are respectively

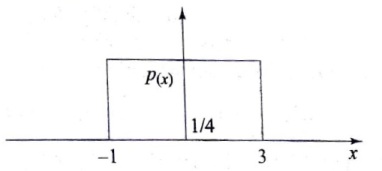
• \frac{1}{2}and\frac{2}{3}
• 1and\frac{4}{3}
• 1and\frac{2}{3}
• 2and\frac{4}{3}

Answer: 1and\frac{4}{3}

15. The spectral density of a real-valued random process has

• an even symmetry
• an odd symmetry
• a conjugate symmetry
• no symmetry

Answer: an even symmetry

16. If the variance \sigma _{x}^{2} of d_{n}=x_{n}-x_{n-1} is one-tenth of variance \sigma _{x}^{2} of a stationary zero-mean discrete time signal x(0, then the normalized autocorrelation function R_{XX(K)}/\sigma _{x}^{2} at K= 1 is

• 0.95
• 0.90
• 0.10
• 0.05

Answer: 0.95

17. Let Y and Z be the random variables obtained by sampling X_{(t)} at t = 2 and t = 4 respectively. Let W = Y- Z. The variance of W is 

• 13.36
• 9.36
• 2.64
• 8.00

Answer: 2.64

18. A random process obeys Poisson’s distribution. It is given that the mean of the process is 5. Then the variance of the process is

• 5
• 0.5
• 25
• 0

Answer: 5

19. A ternary 5 source produces alphabets A, B and C with probabilities P_A = P_B = p and P_C. Which one of the following gives correct values for the maximum value of the entropy of the source and the corresponding value of p and the range of p?  

• 1.58. 0.33, (0, 0.5)
• 1.0, 0.5, (0, 1)
• 3.0. 0.67, (0, 0.5)
• 2.0, 4.2, (0, 0.3)

Answer: 3.0. 0.67, (0, 0.5)

20. An output of a communication channel is a random variable v with the probability density function as shown in the figure. The mean square value of v is

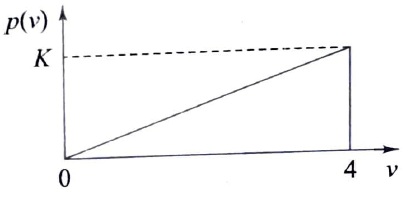
• 4
• 6
• 8
• 9

Answer: 8

21. If E denotes expectation, the variance of a random variable X is given by

• E(X²) – E²(X)
• E(X²) + E²(X)
• E(X²)
• E²(X)

Answer: E(X²) – E²(X)

22. Which one of the following is the correct statement? If the value of a resistor creating thermal noise is doubled, the noise generated is

• halved
• doubled
• unchanged
• slightly changed

Answer: unchanged

23. P_{X}(x)=Me^{-2|x|}+Ne^{-3|x|} is the PDF for the real random variable X over the entire x axis. M and N are both positive real numbers. The equation relating M and N is

• M+\frac{2}{3}N=1
• 2M+\frac{1}{3}N=1
• M+N=1
• M+N=3

Answer: M+\frac{2}{3}N=1

24. A fair coin is tossed 10 times. What is the probability that ONLY the first two tosses will yield heads?

• (\frac{1}{2})
• 10_{C_{2}}(\frac{1}{2})^{2}
• (\frac{1}{2})^{10}
• 10_{C_{2}}(\frac{1}{2})^{10}

Answer: (\frac{1}{2})^{10}

 25. Consider two independent random variables X and Y with identical distributions. The variables X and Y take values 0, 1 and 2 with probabilities ½, ¼, and 1/4 respectively. What is the conditional probability P_{(X+Y=2/X=Y=0)}?

• 0
• 1/16
• 1/6
• 1

Answer: 1/6

26. A discrete random variable X takes values from 1 to 5 with probabilities as shown in the table. A student calculates the mean of X as 3.5 and her teacher calculates the variance X as 1.5. Which of the following statements is true?

K	1	2	3	4	5
P(X=K)	0.1	0.2	0.4	0.2	0.1

• Both the student and the teacher are right.
• Both the student and the teacher are wrong.
• The student is wrong but the teacher is right.
• The student is right but the teacher is wrong.

Answer: Both the student and the teacher are wrong.

27. A fair coin is tossed independently four times. The probability of the event “the number of times heads show up is more than the number of times tails show up” is

• 1/16
• 1/8
• 1/4
• 5/16

Answer: 5/16

28. A fair dice is tossed two times. The probability that the second toss results in a value that is higher that the first toss is

• 2/36
• 2/6
• 5/12
• 1/2

Answer: 5/12

29. Given that f(y)=|y|/y and q is any non-zero real number, the value of [f_{(q)}-f_{(-q)}] is

• 0
• -1
• 1
• 2

Answer: 2

30. Three friends R, S, and T shared toffees from a bowl. R took 1/3rd of the toffees but returned four to the bowl. S took 1/4th of what was left but returned three toffees to the bowl. T took half of the remainder but returned two back in the bowl. If the bowl had 17 toffees left, how many toffees were originally there in the bowl?

• 38
• 31
• 48
• 41

Answer: 48

31. There are two candidates P and Q in an election. During the campaign, 40% of the voters promised to vote for P and the rest, for Q. However, on the day of the election, 15% of the voters went back on their promise to vote for P and voted for Q. 25% of the voters went back on their promise to vote for Q and instead voted for P. Suppose P lost by 2 votes, then what was the total number of voters?

• 100
• 110
• 90
• 95

Answer: 100

32. The classical approach for probability theory does not explain the situation when the number of outcomes of an experiment is small.

• True
• False

Answer: False

33. Mutually exclusive events are also statistically independent.

• True
• False

Answer: False

34. The probability that a continuous random variable takes on a particular value is zero.

• True
• False

Answer: True

35. Unit of variance is same as that of the random variable.

• True
• False

Answer: False